Questions involving motion in a lift

You may often encounter questions involving motion in a lift. Generally such questions are simple, but you should have no confusion in this context. So keep the following points in mind:
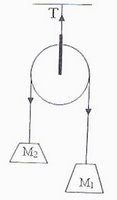
The weight of a body of mass ‘m’ in a lift can be remembered as m(g-a) in all situations if you apply the proper sign to the acceleration ‘a’ of the lift. The acceleration due to gravity ‘g’ always acts vertically downwards and its sign is taken as positive. The following cases can arise in this connection:
(1) Lift moving down with acceleration of magnitude ‘a’:
In this case ‘a’ also is positive and the weight is m(g-a) which is less than the real weight of the body (when it is at rest).
(2) Lift moving up with acceleration:
In this case ‘a’ is negative and the weight is m[g-(-a)] = m(g+a).
(3) Lift moving down with retardation (going to stop while moving down):
In this case also ‘a’ is negative and the weight is m[g-(-a)] = m(g+a) which is greater than the actual weight.
(4) Lift moving up with retardation (going to stop while moving up):
In this case ‘a’ is positive and the weight is m(g-a)
(5) Lift moving up or down with uniform velocity:
In this case ‘a’ is zero and the weight is mg.
(6) Lift moving down with acceleration of magnitude ‘g’ (falling freely under gravity as is the case when the rope carrying the lift breaks):
In this case ‘a’ is positive and the weight is m(g-g) which is zero.
Let us now consider the following question:

A light, frictionless pulley is suspended from the ceiling using a light string. Another light string is passed over the pulley. If unequal masses M₁ and M₂ (M₁ >M₂) are attached to the ends of this string and the system is released, what will be tension ‘T’ in the string that carries the pulley?
(a) (M₁+M₂)g (b) (M₁- M₂)g (c) M₁M₂g/(M₁+M₂) (d) 2M₁M₂g/(M₁+M₂) (e) 4M₁M₂g/(M₁+M₂)

The tension in the string that caries the pulley is due to the weights of the masses m1 and m2. But these weights are not M1g and M2g but M₁(g-a) and M₂(g+a) because M₁ is moving down with acceleration ‘a’ and M2 is moving up with acceleration ‘a’. The magnitude of ‘a’ is given by
a = Net driving force/ Total mass moved = (M1- M2)g/(M1+M2)
Therefore, tension, T = M₁(g-a) + M₂(g+a) = 4M₁M₂g/(M₁+M₂) on substituting for ‘a’. The correct option is (e)
Now consider the following simple question:
A man of mass 70 kg records his weight on a weighing scale placed inside a lift. The ratio of the weight of the man recorded when the lift is ascending with a uniform speed of 1m/s to the weight recorded when the lift is descending with a uniform speed of 2m/s will be
(a) 2 (b) 0.5 (c) 3 (d) 1.5 (e) 1
You should note that his weight is the same as his real weight (when he is at rest). There is no distinction between state of rest and uniform motion. To put this in a different manner, the acceleration of the lift is zero and hence his weight is unchanged. The ratio of the weights is therefore equal to unity [Option (e)].
Now consider the following MCQ:
What is the minimum acceleration with which a fire man can slide down a rope whose breaking strength is 80% of his weight?
(a) 0.2g (b) 0.1g (c) ) 0.9g (d) g (e) 1.1g
This is a situation where the fire man has a rope of insufficient strength. He wants to come down from an unsafe height. He can use the rope to slide down with acceleration so that his weight is reduced (as in a lift moving down with acceleration). His minimum acceleration ‘a’ is given by
m(g-a) = 0.8mg
We have equated his reduced weight to the breaking strength of the rope. The value of ‘a’ is 0.2g [Option (a)]. Note that the rope will break if the acceleration of the fire man is less than this and also that he can use a weaker rope if his acceleration is greater than this.

Multiple Choice Questions on Matter Waves

The following MCQ on de Broglie waves appeared in Kerala Medical Entrance 2004 test paper:
An electron and a proton have the same de Broglie wave length. Then the kinetic energy of the electron is
(a) zero (b) infinity (c) equal to the kinetic energy of the proton (d) greater than the kinetic energy of the proton (e) none of these
Since the de Broglie wave length λ is given by λ = h/p where ‘h’ is Planck’s constant and ‘p’ is the linear momentum, we have p = h/λ. Therefore, the proton and the electron given in the question have the same linear momentum. The kinetic energy (E) is given by E = p²/2m. Since the mass (m) of the electron is less than that of the proton, it follows that the kinetic energy of the electron is greater [Option (d)].
Now consider the following MCQ:
A nucleus of mass ‘M’ at rest emits an α-particle of mass ‘m’. The de Broglie wave lengths of the α-particle and residual nucleus will be in the ratio
(a) m : M (b) (M+m) : m (c) M : m (d) √m:√M (e) 1 : 1
After the α-emission, the α-particle and the residual nucleus will fly off in opposite directions in accordance with the law of conservation of linear momentum. Since the momenta are equal in magnitude, the de Broglie wave lengths are the same and the ratio is 1:1 [Option (e)].
The following MCQ tests your basic knowledge regarding the electron orbits in the hydrogen atom:
The ratio of the de Broglie wave lengths of the electron in the first and the third orbits in the hydrogen atom is
(a) 1 : 1 (b) 1 : 3 (c) 1 : 9 (d) 1 : 6 (e) 1 : 27
You should remember that the orbit of quantum number ‘n’ is made of ‘n’ complete waves so that we have generally 2πr_n = nλ_n where r_nn is the radius of the nth orbit and λ_nn is the wave length of the electron in the n^th orbit. So, we have 2πr₁ = λ₁ for the first orbit and 2πr₃ = 3×λ₃ for the third orbit. Therefore λ₁/λ₃ = 3r₁/ r₃.
But the orbital radius ‘r’ is directly proportional to n². Therefore, λ₁/λ₃ = 3/9 = ⅓. The correct option is (b).
Now consider the following MCQ:
The kinetic energy of an electron is the same as that of a photon of wave length 3100 A.U. What is the wave length of this electron?
(a) 4 A.U. (b) 5.4 A.U. (c) 6.1 A.U. (d) 7.6 A.U. (e) 12.4 A.U.
In the case of a photon, the product λE = 12400 where the wave length λ is in Angstrom Unit (A.U.) and the energy E is in electron volt. Therefore, the energy of the photon of wave length 3100 A.U. is 12400/3100 = 4eV. Since the kinetic energy of the electron is the same as that of the photon, it follows that the kinetic energy of the electron is 4eV, which means this electron was accelerated by 4 volts. The wave length of an electron accelerated by ‘V’ volt is √(150/V) A.U. The answer to the problem is thus √(150/4) A.U. = √(37.5) = 6.1 A.U. approximately [Option (c)].
[You should remember that you can use the above simple relation for the wave length of an electron at small accelerating voltages only (in other words, at non-relativistic speeds only)].

Questions on Communication Systems

Let us discuss the following multiple choice question which appeared in the Kerala Engineering entrance 2005 test paper:
If a radio receiver is tuned to 855kHz radio wave, the frequency of local oscillator in kHz is
(a) 1510 (b) 455 (c) 1310 (d) 1500 (e) 855

Since the radio frequency mentioned in the question is 855 kHz, it must an AM (amplitude modulation) receiver. AM receivers are super heterodyne receivers with intermediate frequency (IF) equal to 455 kHz, by convention.. So the local oscillator in the receiver has a frequency higher by 455 kHz compared to the frequency of the received radio wave. Its frequency is therefore (855+455) kHz = 1310 kHz.
Consider the following MCQ which high lights the component frequencies in an AM wave:
A carrier of frequency 1.2 MHz is amplitude modulated by a microphone output of frequency 800 Hz. The frequencies present in the amplitude modulated carrier are (in kHz)
(a)1.2 MHz and 800 Hz (b) 400 kHz, 1.2 MHz and 2 MHz (c)1.04 MHz,1.2 MHz and 2 MHz (d) 1.1992 MHz, 1.2 MHz and 1.2008 MHz (e) 1.1992 MHz and 1.2008 MHz
The correct option is (d) since the AM wave contains the carrier frequency, the upper side frequency (which is the sum of the carrier frequency and the modulating signal frequency) and the lower side frequency (which is the difference between the carrier frequency and the modulating signal frequency). While finding the upper and lower side frequencies, it will be convenient if you convert the frequencies in to kilohertz or megahertz. Thus, the lower side frequency = (1200 – 0.8)kHz = 1199.2 kHz = 1.1992 MHz. Similarly, the upper side frequency = (1200 + 0.8) kHz = 1200.8 kHz = 1.2008 MHz.
Now consider the following question:
A semiconductor is to be selected for use as a photo detector to detect radiation of wavelength 620 nm. The appropriate semiconductor will have a band gap of
(a) 2eV (b) 2.2eV (c) 2.4eV (d) 2.8eV (e) both (a) and (b)
The band gap of the semiconductor should not exceed the energy of the photon. The wavelength of the photon being 620 nm which is equal to 6200 Angstrom Units (A.U), its energy is 12400/6200 = 2.0 eV (Note that the product of the wave length in A. U. and the energy in eV for a photon is 12400). The option (a) alone is therefore suitable.
The following MCQ appeared in Kerala Engineering Entrance 2006 test paper:
If α and β are the current gains in the CB and CE configurations respectively of the transistor circuit, then (β – α)/αβ =
(a) ∞ (b) 1 (c) 2 (d) 0.5 (e) zero
Since β = α/(1- α), the given ratio, (β – α)/αβ =[α/(1- α) – α]/αβ = [1/(1- α) -1]/β =[1-(1- α)]/(1-α)β = α/(1- α)β = β/β =1. So, the correct option is (b).