Birla Institute of Technology & Science (BITS) -- BITSAT-2007

The BITSAT-2007 Online tests (for admission to the academic year 2007-08) will be conducted during 7th May - 10th June 2007. These tests are for admitting students to the Integrated First Degree Programmes. You will find details here

MCQ on Semiconductor Devices

The following simple question appeared in Kerala Medical Entrance 2006 Test paper:

A PN junction diode is connected to a battery of emf 5.5 V and external resistance 5.1 kΩ. The barrier potential in the diode is 0.4 V. The current in the circuit is
(a) 1.08 mA (b) 0.08 mA (c) 1 mA (d) 1 A (e) 2 mA

Out of 5.5 volts, 0.4 volt (barrier potential) is dropped across the forward biased diode and the remaining 5.1 volts appears across the 5.1 kΩ resistance. So, the current through the resistance is (5.1V/5.1kΩ), which is equal to 1mA [Option (c)].
The following MCQ on half wave rectifier also is simple:
A sinusoidal voltage of peak to peak value 310 V is connected in series with a diode and a load resistance R so that half wave rectification occurs. If the diode has negligible forward resistance and very high reverse resistance, the r.m.s. voltage across the load resistance is
(a) 310 V (b) 155 V (c) 219 V (d)109.5 V (e) 77.5 V
If V_m is the peak value (maximum value) of an alternating voltage, its r.m.s. value is Vm/√2. The r.m.s. value of full wave rectifier output also is V_m/√2. Therefore, the mean square value of the full wave rectifier output is V_m²/2. The mean square value of the half wave rectifier output is half of this, which is equal to V_m²/4. Therefore, r.m.s. value of half wave rectifier output voltage is V_m/2.
Note that the peak to peak value (310 V) is given in the question. The peak value V_m is 155 volts and hence the r.m.s. value is 155/2 = 77.5 V.
Here is a question which may confuse you and you may be tempted to pick out the wrong answer:
A common emitter low frequency amplifier has a collector supply voltage (V_CC) of 9 V. The amplifier has input resistance 1kΩ and collector load resistance 5 kΩ. The transistor used has a common emitter current gain (β) of 100. What will be the peak to peak output signal voltage if an input peak to peak signal voltage of 50 mV from a low impedence source is applied to this amplifier?
(a) 250 V (b) 25 V (c) 18 V (d) 12.5 V (e) 9 V
The voltage gain (amplification) of the amplifier is, A_v = β (R_L/R_i) where β is the common emitter current gain, R_L is the load resistance and Ri is the input resistance.Therefore, A_v = 100×5/1 = 500.
( Note that questions on calculation of voltage gain are often seen in Medical and Engineering Entrance test papers. They are simple to solve at Higher Secondary and Plus Two levels, as we hve done above).
The important thing to remember (especially in the context of the present question) is that you will get the full gain only if the input voltage is small. If the input voltage were 5 mV peak to peak for instance, you would have obtained a peak to peak output voltage of 500 times the input voltage, which is 500×5 mV = 2500 mV = 2.5 V.
But since the input is 50 mV, you cannot obtain 500×50 mV (= 25000 mV = 25 V) for the simple reason that the collector supply voltage is 9 volts only. The maximum possible peak to peak signal voltage will be 9 volts only given in option (e).
[The transistor will swing between saturation and cut off as the signal voltage swings between the positive and negative peaks and you will get a clipped output signal which has a peak to peak value of approximately 9 volts in the present case].

You will find more multiple choice questions in this section at physicsplus: Multiple Choice Questions from Electronics

Spring Constant and Potential Energy of Spring

Spring constant (force constant of a spring) is the force required for unit extension (or contraction) in a spring. Suppose a spring is cut into two pieces of equal length. Will the spring constant change? Don’t be doubtful. The spring constant will be doubled. If you cut a spring of spring constant ‘k’ into ‘n’ pieces of equal length, the spring constant of each piece will be nk.
Springs may appear in series and parallel combinations in certain questions, as for example, in problems involving the period of oscillation of a spring-mass system. If you have springs of constants k₁, k₂, k₃….etc. in series, the net spring constant ‘k’ of the combination is given by the reciprocal relation, 1/k = 1/k₁ + 1/k₂ + 1/k₃ + . . . . . . .etc.
If you have springs in parallel, the net spring constant ‘k’of the combination is given by k = k₁+ k₂+ k₃+ . . . . .etc.
Often you will encounter questions involving the potential energy of a spring. You should remember that the potential energy of a spring of constant ‘k’, stretched (or contracted) through a distance ‘x’ is (½) kx². Consider the following MCQ:
When a long spiral spring is stretched by 2 cm, its potential energy is U. If the spring is stretched by 6 cm, its potential energy will be
(a) 3U (b) 6U (c) 9U (d) U (e) 36U
Since the potential energy is ½ kx², it follows that the P.E. is directly proportional to the square of the stretch (extension). The extension being 3 times, the P.E. must be 9 times. So, the correct option is (c).
Suppose the above question is asked in the following modified form:
When a long spiral spring is stretched by 2 cm, its potential energy is U. If the spring is stretched by 6 cm, the increase in its potential energy will be
(a) 4U (b) 6U (c) 9U (d) 8U (e) 36U
Since the difference between the initial and final potential energies is required in this problem, the answer is 9U-U = 8U.
Now, consider the following question:
The tension in a spring of spring constant k is T. The potential energy of the spring is
(a) T²/k² (b) T²/k (c) 2T²/k (d) T²/2k (e) 2T²/k²
Potential energy of a spring, as you know, is (½)kx². But k=T/x from which x=T/k. On substituting this value of x in the expression for potential energy, we obtain option (d) as the answer.
Now, consider the following M.C.Q. which appeared in IIT screening 2002question paper:
An ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially un-stretched. Then the maximum extension in the spring is
(a) 4Mg/k (b) 2Mg/k (c)Mg/k (d) Mg/2k
When the mass is released, its gravitational potential energy is decreased and the elastic potential energy in the spring is increased by an equal amount. If ‘x’ is the maximum extension produced (when the mass reaches the lowest position), we have Mgx = (½) kx², from which x = 2Mg/k. [Option (b)]

All India Engineering/Architecture Entrance Examination (AIEEE) 2007

Application Form and the Information Bulletin of the All India Engineering/Architecture Entrance Examination 2007 to be conducted by Central Board of Secondary Education (CBSE) on 29th April 2007 will be distributed from 1-12-2006 to 5-1-2007. The Information Bulletin and the Application Form can be obtained personally from designated branches of Syndicate Bank/Institutions and Regional Offices of CBSE. Designated branches of Syndicate Bank in Kerala are:

(1) Thiruvananthspuram- Syndicate Bank, Co-operative Agriculture and Rural Development Bank Building, P .B.No.314, Thiruvananthapuram-695001

(2) Ernakulam- Syndicate Bank, Pioneer Towers, First Floor, P.B.No.2616, Shanmugham Road, Ernakulam-682031

(3) Kozhikode- Syndicate Bank, P.B.No.61, Cherootty road, Kozhikode-673001

(4) Kottayam- Syndicate Bank,, P.B.No.121, Baker Junction, Kottayam-686001

(5) Trichur- Syndicate Bank, Palace Road, Trichur-680020

The Information Bulletin and the Application form can be obtained by post from the Joint Secretary (AIEEE), Central Board of secondary Education, 17, Rouse Avenue, Institutioal Area (Near Bal Bhavan), New Delhi-110002.

The cost of Information Bulletin containing the Application Form, inclusive of the examination fee for BE/B.Tech. only or B.Arch/B.Planning only is Rs.300/- and Rs.150/- for General and SC/ST candidates respectively. Candidates appearing for both BE/B.Tech and B.Arch/B.Planning together should send their application form along with additional fee in the form of Demand Draft of Rs.200/- for General and Rs.100/- for SC/ST candidates in favour of Secretary, CBSE, payable at Delhi/New Delhi.
To obtain Information Bulletin containing Application Form by post, candidates should send their request to The Joint Secretary (AIEEE), Central Board of Secondary Education, 17, Rouse Avenue, Institutional Area (Near Bal Bhavan), New Delhi-110002, along with a bank draft of Rs.350/- for General Category and Rs.200/- for SC/ST candidates in favour of The Secretary, CBSE, payable at Delhi/New Delhi and a self addressed envelope of 12”×10”.

Important information at a glance:

(1) a. Sale of AIEEE Information Bulletin containing Application Form - 01.12.2006 to 05.01. 2007

b. Online submission of application on website http://www.aieee.nic.in/ - 01.12.2006 to 05.01.2007

(2) Last date for
a. Receipt of request for Information Bulletin and Application Form by Post at CBSE Office, Shiksha Sadan, 17, Rouse Avenue, Institutional Area, (Near Bal Bhawan), New Delhi-110002 - 25.12.2006

b. Sale of Information Bulletin at designated branches of Syndicate Bank, Regional Offices of the CBSE and designated institutions - 05.01.2007

c. Online submission of applications - 05.01.2007

d. Receipt of complete applications “by post” including Registration Forms with Bank Draft at AIEEE Unit, CBSE, Shiksha Sadan, 17, Rouse Avenue, Institutional Area, (Near Bal Bhawan), New Delhi – 110002 -
10.01.2007

(3) Date of dispatch of Admit Card - 09.03.2007 to 26.03.2007
(4) Issue/dispatch of duplicate admit card(on request only with fee of Rs. 50/- + postal charges of Rs. 30/- extra for out station candidate): - 10.04.2007 to 29.04.2007 (By Hand)
- 10.04.2007 to 20.04.2007 (By Post)

(5) Dates of Examination

PAPER – 1: 29.04.2007 (0930-1230 hrs)

PAPER – 2: 29.04.2007 (1400-1700 hrs)
Visit the site www.aieee.nic.in for complete information including details of ‘online’ application, extra information for candidates opting for examination centres in foreign countries, syllabus etc.

Questions involving motion in a lift

You may often encounter questions involving motion in a lift. Generally such questions are simple, but you should have no confusion in this context. So keep the following points in mind:
The weight of a body of mass ‘m’ in a lift can be remembered as m(g-a) in all situations if you apply the proper sign to the acceleration ‘a’ of the lift. The acceleration due to gravity ‘g’ always acts vertically downwards and its sign is taken as positive. The following cases can arise in this connection:
(1) Lift moving down with acceleration of magnitude ‘a’:
In this case ‘a’ also is positive and the weight is m(g-a) which is less than the real weight of the body (when it is at rest).
(2) Lift moving up with acceleration:
In this case ‘a’ is negative and the weight is m[g-(-a)] = m(g+a).
(3) Lift moving down with retardation (going to stop while moving down):
In this case also ‘a’ is negative and the weight is m[g-(-a)] = m(g+a) which is greater than the actual weight.
(4) Lift moving up with retardation (going to stop while moving up):
In this case ‘a’ is positive and the weight is m(g-a)
(5) Lift moving up or down with uniform velocity:
In this case ‘a’ is zero and the weight is mg.
(6) Lift moving down with acceleration of magnitude ‘g’ (falling freely under gravity as is the case when the rope carrying the lift breaks):
In this case ‘a’ is positive and the weight is m(g-g) which is zero.
Let us now consider the following question:

A light, frictionless pulley is suspended from the ceiling using a light string. Another light string is passed over the pulley. If unequal masses M₁ and M₂ (M₁ >M₂) are attached to the ends of this string and the system is released, what will be tension ‘T’ in the string that carries the pulley?
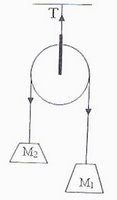
(a) (M₁+M₂)g (b) (M₁- M₂)g (c) M₁M₂g/(M₁+M₂) (d) 2M₁M₂g/(M₁+M₂) (e) 4M₁M₂g/(M₁+M₂)

The tension in the string that caries the pulley is due to the weights of the masses m1 and m2. But these weights are not M1g and M2g but M₁(g-a) and M₂(g+a) because M₁ is moving down with acceleration ‘a’ and M2 is moving up with acceleration ‘a’. The magnitude of ‘a’ is given by
a = Net driving force/ Total mass moved = (M1- M2)g/(M1+M2)
Therefore, tension, T = M₁(g-a) + M₂(g+a) = 4M₁M₂g/(M₁+M₂) on substituting for ‘a’. The correct option is (e)
Now consider the following simple question:
A man of mass 70 kg records his weight on a weighing scale placed inside a lift. The ratio of the weight of the man recorded when the lift is ascending with a uniform speed of 1m/s to the weight recorded when the lift is descending with a uniform speed of 2m/s will be
(a) 2 (b) 0.5 (c) 3 (d) 1.5 (e) 1
You should note that his weight is the same as his real weight (when he is at rest). There is no distinction between state of rest and uniform motion. To put this in a different manner, the acceleration of the lift is zero and hence his weight is unchanged. The ratio of the weights is therefore equal to unity [Option (e)].
Now consider the following MCQ:
What is the minimum acceleration with which a fire man can slide down a rope whose breaking strength is 80% of his weight?
(a) 0.2g (b) 0.1g (c) ) 0.9g (d) g (e) 1.1g
This is a situation where the fire man has a rope of insufficient strength. He wants to come down from an unsafe height. He can use the rope to slide down with acceleration so that his weight is reduced (as in a lift moving down with acceleration). His minimum acceleration ‘a’ is given by
m(g-a) = 0.8mg
We have equated his reduced weight to the breaking strength of the rope. The value of ‘a’ is 0.2g [Option (a)]. Note that the rope will break if the acceleration of the fire man is less than this and also that he can use a weaker rope if his acceleration is greater than this.

Multiple Choice Questions on Matter Waves

The following MCQ on de Broglie waves appeared in Kerala Medical Entrance 2004 test paper:
An electron and a proton have the same de Broglie wave length. Then the kinetic energy of the electron is
(a) zero (b) infinity (c) equal to the kinetic energy of the proton (d) greater than the kinetic energy of the proton (e) none of these
Since the de Broglie wave length λ is given by λ = h/p where ‘h’ is Planck’s constant and ‘p’ is the linear momentum, we have p = h/λ. Therefore, the proton and the electron given in the question have the same linear momentum. The kinetic energy (E) is given by E = p²/2m. Since the mass (m) of the electron is less than that of the proton, it follows that the kinetic energy of the electron is greater [Option (d)].
Now consider the following MCQ:
A nucleus of mass ‘M’ at rest emits an α-particle of mass ‘m’. The de Broglie wave lengths of the α-particle and residual nucleus will be in the ratio
(a) m : M (b) (M+m) : m (c) M : m (d) √m:√M (e) 1 : 1
After the α-emission, the α-particle and the residual nucleus will fly off in opposite directions in accordance with the law of conservation of linear momentum. Since the momenta are equal in magnitude, the de Broglie wave lengths are the same and the ratio is 1:1 [Option (e)].
The following MCQ tests your basic knowledge regarding the electron orbits in the hydrogen atom:
The ratio of the de Broglie wave lengths of the electron in the first and the third orbits in the hydrogen atom is
(a) 1 : 1 (b) 1 : 3 (c) 1 : 9 (d) 1 : 6 (e) 1 : 27
You should remember that the orbit of quantum number ‘n’ is made of ‘n’ complete waves so that we have generally 2πr_n = nλ_n where r_nn is the radius of the nth orbit and λ_nn is the wave length of the electron in the n^th orbit. So, we have 2πr₁ = λ₁ for the first orbit and 2πr₃ = 3×λ₃ for the third orbit. Therefore λ₁/λ₃ = 3r₁/ r₃.
But the orbital radius ‘r’ is directly proportional to n². Therefore, λ₁/λ₃ = 3/9 = ⅓. The correct option is (b).
Now consider the following MCQ:
The kinetic energy of an electron is the same as that of a photon of wave length 3100 A.U. What is the wave length of this electron?
(a) 4 A.U. (b) 5.4 A.U. (c) 6.1 A.U. (d) 7.6 A.U. (e) 12.4 A.U.
In the case of a photon, the product λE = 12400 where the wave length λ is in Angstrom Unit (A.U.) and the energy E is in electron volt. Therefore, the energy of the photon of wave length 3100 A.U. is 12400/3100 = 4eV. Since the kinetic energy of the electron is the same as that of the photon, it follows that the kinetic energy of the electron is 4eV, which means this electron was accelerated by 4 volts. The wave length of an electron accelerated by ‘V’ volt is √(150/V) A.U. The answer to the problem is thus √(150/4) A.U. = √(37.5) = 6.1 A.U. approximately [Option (c)].
[You should remember that you can use the above simple relation for the wave length of an electron at small accelerating voltages only (in other words, at non-relativistic speeds only)].

Questions on Communication Systems

Let us discuss the following multiple choice question which appeared in the Kerala Engineering entrance 2005 test paper:
If a radio receiver is tuned to 855kHz radio wave, the frequency of local oscillator in kHz is
(a) 1510 (b) 455 (c) 1310 (d) 1500 (e) 855

Since the radio frequency mentioned in the question is 855 kHz, it must an AM (amplitude modulation) receiver. AM receivers are super heterodyne receivers with intermediate frequency (IF) equal to 455 kHz, by convention.. So the local oscillator in the receiver has a frequency higher by 455 kHz compared to the frequency of the received radio wave. Its frequency is therefore (855+455) kHz = 1310 kHz.
Consider the following MCQ which high lights the component frequencies in an AM wave:
A carrier of frequency 1.2 MHz is amplitude modulated by a microphone output of frequency 800 Hz. The frequencies present in the amplitude modulated carrier are (in kHz)
(a)1.2 MHz and 800 Hz (b) 400 kHz, 1.2 MHz and 2 MHz (c)1.04 MHz,1.2 MHz and 2 MHz (d) 1.1992 MHz, 1.2 MHz and 1.2008 MHz (e) 1.1992 MHz and 1.2008 MHz
The correct option is (d) since the AM wave contains the carrier frequency, the upper side frequency (which is the sum of the carrier frequency and the modulating signal frequency) and the lower side frequency (which is the difference between the carrier frequency and the modulating signal frequency). While finding the upper and lower side frequencies, it will be convenient if you convert the frequencies in to kilohertz or megahertz. Thus, the lower side frequency = (1200 – 0.8)kHz = 1199.2 kHz = 1.1992 MHz. Similarly, the upper side frequency = (1200 + 0.8) kHz = 1200.8 kHz = 1.2008 MHz.
Now consider the following question:
A semiconductor is to be selected for use as a photo detector to detect radiation of wavelength 620 nm. The appropriate semiconductor will have a band gap of
(a) 2eV (b) 2.2eV (c) 2.4eV (d) 2.8eV (e) both (a) and (b)
The band gap of the semiconductor should not exceed the energy of the photon. The wavelength of the photon being 620 nm which is equal to 6200 Angstrom Units (A.U), its energy is 12400/6200 = 2.0 eV (Note that the product of the wave length in A. U. and the energy in eV for a photon is 12400). The option (a) alone is therefore suitable.
The following MCQ appeared in Kerala Engineering Entrance 2006 test paper:
If α and β are the current gains in the CB and CE configurations respectively of the transistor circuit, then (β – α)/αβ =
(a) ∞ (b) 1 (c) 2 (d) 0.5 (e) zero
Since β = α/(1- α), the given ratio, (β – α)/αβ =[α/(1- α) – α]/αβ = [1/(1- α) -1]/β =[1-(1- α)]/(1-α)β = α/(1- α)β = β/β =1. So, the correct option is (b).

Direct Current Circuits

The following simple question appeared in Kerala Medical Entrance 2006 test paper:
Four cells each of emf 2V and internal resistance 1Ω are connected in parallel to a load resistor of 2Ω. Then the current through the load resistor is
(a) 2A (b) 1.5A (c) 1A (d) 0.888A (e) 0.75A
Since the cells are connected in parallel, the internal resistance of the combination is 1/4=0.25Ω. If ‘R’ is the load resistance and ‘r’ is the internal resistance, the current through load resistance= V/(R+r) = 2/(2+0.25) = 0.888A. So (d) is the correct option.
Now consider the following M.C.Q. which appeared in the question paper of Karnataka C.E.T.2003:
Two wires of the same dimensions but resistivities ρ₁ and ρ₂ are connected in series. The equivalent resistivity of the combination is
(a) 2(ρ₁ + ρ₂) (b) √(ρ₁ρ₂) (c) (ρ₁ + ρ₂)/2 (d) ρ₁ + ρ₂
If R₁ and R₂ are the resistances of the wires, R₁ = ρ₁L/A and R = ρ₂L/A where L and A are the length and the cross section area respectively. When the wires are connected in series the total length is 2L and the total resistance is R₁ + R₂. Hence the resistivity of the combination is given by ρ = (R₁ + R₂)A/2L = (R₁A/2L) + (R₂A/2L) = ρ₁/2 + ρ₂/2. The correct option therefore is (c).
Suppose we make this question a bit more complicated by making the lengths of the two wires different (say, L₁ and L₂). Then, ρ = (R₁ + R₂)A/(L₁ + L₂) = [(ρ₁L₁/A) + (ρ₂ L₂/A)] A/(L₁ + L₂) = (ρ₁L₁ + ρ₂L₂)/(L₁ + L₂).
Now, consider the following question:
The heat produced per second in a 2Ω resistor on connecting it across a battery is the same as the heat produced per second in an 8Ω resistor on connecting it across the same battery after disconnecting the 2Ω resistor. The internal resistance of the battery is
(a) 4Ω (b) 5Ω (c) 6Ω (d) √10 Ω (e) 3.3Ω
It is convenient to remember the internal resistance as √(R1R2) in situations like this. The answer is √(2×8) = 4 Ω. You can work it out from ‘first principles’ like this:
The currents through the resistors in the two cases are V/(2 + r) and V/(8 + r) with usual notations. Equating the powers (I2R values), we have, [V/(2 + r)]2×2 = [V/(8 + r)]2×8, from which r = 4 Ω.
Let us consider the following question also taken from Karnataka C.E.T.2003 question paper:
If a 30V, 90W bulb is to be worked on 120V line, the resistance to be connected in series with the bulb is
(a) 40 Ω (b) 30 Ω (c) 20 Ω (d) 10 Ω
30V, 90W bulb means the power consumed by the bulb on connecting it across a 30volt supply is 90 watt. The current drawn by this bulb (while incandescent) is 90watt/30 volt = 3 ampere and the resistance of this bulb is 30V/3A = 10 Ω. The problem is basically to find out the resistance required to limit the current to 3A. If R is the resistance required in series with the bulb, we have, 120volt/(10 + R)ohm = 3 ampere. Therefore, R = 30 Ω.

All India Pre-Medical/Pre-Dental Entrance Examination (AIPMT) 2007- Dates Announced

Central Board of Secondary Education (CBSE), Delhi has announced the dates pertaining to the All India Pre-Medical/Pre-Dental Entrance Examination (AIPMT) 2007 for admission to 15% of the total seats for Medical/Dental Courses in all Medical/Dental colleges run by the Union of India, State Governments and Municipal or other local authorities in India except in the States of ANDHRA PRADESH AND JAMMU & KASHMIR. The dates of the Examination are:
(1) Preliminary Examination : 1st April 2007 (Sunday)
(2) Final Examination : 13th May 2007 (Sunday)

The Information Bulletin and Application Form costing Rs.400/- for General Category candidates and Rs.200/- for SC/ST candidates inclusive of examination fee can be obtained against Cash Payment from designated branches of Canara Bank and Regional Offices of CBSE up to 18-11-2006. Designated branches of Canara Bank in Kerala are:
KOTTAYAM : P.B. No.122, K.K.Road, Kottayam-686 001

QUILANDY : Fasila Buidling, Main Road, Quilandy-673 305

TRIVANDRUM : Ist Floor, Ibrahim Co. Bldg., Challai, Trivandrum-695 023
TRIVANDRUM : Plot no.2, PTP Nagar Trivandrum-695 038
TRIVANDRUM : TC No.25/1647, Devaswom Board Bldg. M.G. Road, Trivandrum-695 001

ERNAKULAM : Shenoy’s Chamber, Shanmugam Road, Ernakulam, Cochin-682 031
CALICUT : 9/367-A, Cherooty Road, Calicut-673 001
TRICHUR : Trichur Main Ramaray Building, Round South, Trichur-680001
QUILON : Maheshwari Mansion, Tamarakulam, Quilon-691 001
PALGHAT : Market Road, Big Bazar, 20/68, Ist floor,Palghat-678 014.

The Information Bulletin and Application Form can also be obtained by Speed Post/Registered Post by sending a written request with a Bank Draft/Demand Draft for Rs.450/- for General Category and Rs.250/- for SC/ST Category payable to the Secretary, Central Board of Secondary Education, Delhi along with a Self Addressed Envelope of size 12” x 10”. The request must reach the Deputy Secretary (AIPMT), CBSE, 2, Community Centre, Preet Vihar, Delhi-110 092 on or before 10-11-2006. The request should be super scribed as “Request for Information Bulletin and Application Form for AIPMT, 2007”.

Completed Application Form is to be dispatched by Registered Post/Speed Post only. Last Date for receipt of completed Application Forms in CBSE is 20-11-2006. You can obtain complete information at www.cbse.nic.in

Rotational Motion – Rolling bodies

If you release from rest differently shaped regular bodies such as disk, ring, hollow sphere, solid sphere, hollow cylinder(pipe) and solid cylinder from the top of an inclined plane, thereby allowing them to roll down the plane, you will find that the solid sphere always arrives at the bottom first and the ring and the pipe arrive last. The acceleration ‘a’ of a body of radius ‘R’ rolling down an inclined plane (without slipping) is given by a= g sinθ/[1+( k² / R²)] where ‘g’ is the acceleration due to gravity, ‘θ’ is the angle of the plane and ‘k’ is the radius of gyration given by I= Mk² where ‘I’ is the moment of inertia of the body (of mass M) about the central axis about which it is rolling down. Since the moment of inertia of a solid sphere about its diameter is (2/5) MR², we have (2/5)MR² = Mk². Therefore, k²/R² = 2/5.
The ring and the pipe have k²/R² = 1, since I=MR² = Mk². If you find the values of k²/R² in the case of differently shaped rolling bodies, you will realize that it is minimum (2/5) for the solid sphere and maximum (equal to1) for a thin ring and a thin pipe. Since (k²/R²) appears in the denominator in the expression for ‘a’, the acceleration down the plane is maximum in the case of a solid sphere and minimum in the case of a ring or a pipe. So the solid sphere arrives at the bottom first and the ring and the pipe arrive last.
You should remember that the moment of inertia of a disk (and that of a solid cylinder) about its rolling axis is ½ MR² and that of a hollow sphere is (2/3) MR²
It is interesting to note that all solid spheres will arrive at the bottom together, irrespective of their mass and size. Similarly, all thin rings and thin pipes will arrive together, irrespective of their mass and size. Generally speaking, bodies of a given shape will arrive together, irrespective of their mass and size.
Now, consider the following M.C.Q.:

A body of mass M at the top of a smooth inclined plane starts from rest and slides down the plane. It reaches the bottom with a velocity ‘v’. If the same body were in the form of a ring and the plane were rough, the velocity with which the ring will reach the bottom on rolling down the plane would be
(a) v (b) v√2 (c) 2v (d) v/√2 (e) v/2
Note that if a body is to roll along any surface, friction is necessary and that is why the plane is said to be made rough in the problem. On a smooth plane, the body will slide down with acceleration gsinθ and will reach the bottom with a velocity ‘v’ given by v² = 0 + 2gsinθ×s, as given by the usual equation of linear motion, v² = u² + 2as.
Therefore, v = √(2sgsinθ).
On rolling, the acceleration down the plane is gsinθ/[1 + (k²/R²)] = ½ gsinθ since k²/R² = 1 for a ring. Therefore the velocity (v1) on reaching the bottom is given by v₁² = 0 + 2×½ gsinθ×s
Therefore, v₁ = √(sgsinθ) = v/√2 [Option (d)].

Let us discuss another M.C.Q.:

A sphere of radius ‘R’ is kept at the top end of a curved track. The upper end of the track is at a height ‘H’ and the lower end which is horizontal, is at a height ‘h’ above above the ground level.

When the sphere is released, it rolls down (without slipping) along the track and after leaving the lower end of the track, it moves like a projectile and lands at the point C. The horizontal distance BC is
(a) R√[(20/7)gh(H-h)] (b) √[(20/7)gh(H-h)] (c) √[(10/7)gh(H-h)]
(d) √[(20/7)h(H-h)] (e) √[(5/7)h(H-h)]
The loss of potential energy by the sphere on rolling down along the track is equal to the gain of kinetic energy (both translational and rotational) so that
Mg(H-h) = ½ Mv² + ½ I ω² where M is the mass, ‘v’ is the linear velocity, ‘ω’ is the angular velocity and ‘I’ is the moment of inertia of the sphere, which is (2/5)MR². Substituting for ω = v/R, we obtain v = √[(10/7)g(H-h)]. This is the horizontal velocity of the sphere at the lower end of the track. Since its height at the lower end of the track is ‘h’, the time taken to reach the ground from there is t = √(2h/g). Note that we obtain this time by considering the vertical motion of the sphere and using the equation, h = 0 + ½ gt². The horizontal distance BC = vt = √[(20/7)h(H-h)]. So, (d) is the correct option. Note that this contains neither R nor g.
The following question is a conventional type which you will get in your class examinations as well as in entrance tests:

A solid cylinder of mass M and radius R rolls down an inclined plane of height ‘h’ without slipping after starting from rest at the top. The speed of its centre of mass when it reaches the bottom is
(a) √(2gh) (b) √(4gh/3) (c) √(3gh/4) (d) √(2gh/3) (e) √(3gh/2)
Equating the gravitational potential energy of the cylinder at the top of the plane to the sum of the translational and rotational kinetic energies at the bottom, we have,Mgh = ½ Mv² + ½ I ω² = ½ Mv² + ½ ×½ MR² × (v/R)² = (3/4)Mv², from which v = √(4gh/3).

Here is another typical M.C.Q. involving rotational motion:
A spherical ball rolls on a table without slipping. The fraction of its total energy which is associated with rotational motion is
(a) 3/5 9b) 2/3 (c) 2/5 (d) 3/7 (e) 2/7
The rolling ball has translational and rotational kinetic energies giving it total kinetic energy equal to ½ Mv² + ½ I ω² = ½ Mv² + ½ ×(2/5)MR² × (v/R))² =½ Mv² + (1/5)Mv² = (7/10)Mv².
The rotational kinetic energy is (1/5)Mv² and the total kinetic energy is (7/10)Mv². The required ratio is therefore (1/5) / (7/10) which is 2/7 [Option (e)].

You will see interesting questions (with solution) on rotational motion here as well as here.

If you would like to have still more multiple choice questions (with solution) on rotational motion, you can have them here.

Kinetic energy of gas molecules

Most of you might be remembering the expression for the total average kinetic energy of a gas molecule: E = (n/2)kT where ‘n’ is the number of degrees of freedom, ‘k’ is Boltzman’s constant and T is the absolute temperature. The values for ‘n’ are 3 for mono atomic, 5 for diatomic and 6 for tri and polyatomic gas molecules. [Note that we have not considered the possible vibrational modes of diatomic and polyatomic gas molecules here].
One important thing you have to note is that the average translational kinetic energy of all types of molecules is (3/2)kT since we have a universe with three dimensional space (n=3).
If you consider one mole of gas molecules, the average total kinetic energy (for one mole) is (n/2)RT and the average translational kinetic energy (for one mole) is (3/2)RT where ‘R’ is universal gas constant.
Now, consider the following M.C.Q.:
The average translational kinetic energy of oxygen molecule at a temperature ‘T’ is 6×10^-21 J. The average translational kinetic energy of helium atom at a temperature 2T will be
(a) 3.6×10^-21 J (b) 7.2×10^-21 J (c) 2.88×10^-20 J (d) 6×10^-21 J (e) 1.2×10^-20 J
Since the translational kinetic energy is (3/2)kT for all types of gas molecules, it depends only on temperature and the answer is 1.2×10^-20 J [Option (e)].
The following MCQ high lights the type of the molecule in addition to the temperature you will have to consider while calculating the kinetic energy:
The ratio of the total kinetic energy of all the molecules in one mole of hydrogen at temperature ‘T’ to the total kinetic energy of all the molecules in two moles of helium at temperature 2T is
(a) 5:6 (b) 5:12 (c) 5:3 (d)1:2 (e) 1:4
The total kinetic energies per mole in the case of hydrogen and helium are, respectively, (5/2)RT and (3/2)RT since hydrogen is diatomic and helium is mono atomic. Hence the required ratio is [(5/2)RT] : [2×(3/2)R×2T] = 5:12 [Option (b)].
The following question appeared in the I.I.T.1997 test paper:
The average translational energy and the rms speed of molecules in a sample of oxygen gas at 300 K are 6.21×10^-21J and 484 m/s respectively. The corresponding values at 600 K are nearly (assuming ideal gas behaviour)
(a) 12.42×10^-21J, 968 m/s (b) 8.78×10^-21J, 684 m/s (c) 6.21×10^-21J, 968 m/s (d) 12.42×10^-21J, 684 m/s
Average translational energy per mole = (3/2)RT . When the temperature changes from 300 K to 600 K, the energy is doubled. The rms speed of gas molecules = √(3kT/m) where ‘k’ is Boltzman’s constant and ‘m’ is the molecular mass. So rms speed becomes √2 times when the temperature changes from 300 K to 600 K. The correct option is (d).

You can find more multiple choice questions at physicsplus: Questions on Kinetic Theory of Gases

Questions involving Magnetic Fields

The following M.C.Q. which appeared in the All India Pre –Medical/Dental Entrance-2005 (C.B.S.E) test paper will be interesting to you:
An electron moves in a circular orbit with a uniform speed ‘v’. It produces a magnetic field ‘B’ at the centre of the circle. The radius of the circle is proportional to
(a) √(B/v) (b) B/v (c) √(v/B) (d) v/B
The electron, moving along the circular path is equivalent to a current I = e/T = ev/(2πr) where ‘e’ is the electronic charge, T is the period, ‘v’ is the speed and ‘r’ is the radius of the circular motion. The magnetic field at the centre of the circle, B = μ₀I/2r = μ₀ev/4πr² so that r α √(v/B). The correct option is (c).
Now, consider the following simple question. (Be careful however, so that you won’t pick out a wrong answer):
A long straight conductor P carries a current ‘I’ while another parallel long straight conductor Q carries a current 2I in the same direction. The magnetic field midway between them is B. If the current 2I in the conductor Q is switched off, the magnetic field midway between the conductors will be
(a) B/3 (b) B (c) –B (d) –B/2 (e) 2B
The magnetic fields produced by the conductors are in opposition in the region between them. The field produced by Q is twice the field produced by P. If the field produced by Q is 2B, the field produced by P is –B. This is indeed the case, since the net field is B when both currents are switched on. When the current 2I in Q is switched off, the field due to Q alone is present. The answer therefore is –B [Option (c)].
The following question also is simple. It is designed to check your understanding of certain basic things:
A straight conductor of length ‘L’ carrying a current ‘I’ is bent in the form of a semicircle. The magnetic flux density (in tesla) at the centre of the semicircle is approximately
(a) 10^-6I/L (b) 10-7I/L (c) 10^-6π²I/L (d) 10⁷π²I/L (e) π²I/L
The magnetic field at the centre of a single turn circular current carrying coil is μ₀I/2r and hence the magnetic field at the centre of a semicircle is μ₀I/4r. The radius of the semicircle obtained by bending the straight conductor of length L is, r = L/π. On substituting this value, the magnetic field at the centre of the semicircle is μ₀πI/ 4L. Since μ₀ = 4π ×10^-7, the field is 10^-7π² I/L. But π² is approximately equal to 10 so that the answer is 10^-6I/L [Option (a)].
Let us now consider the following M.C.Q. which appeared in the Karnataka Common Entrance test paper of 2005:
The electrons in the beam of a television tube move horizontally from south to north. The vertical component of the earth’s magnetic field points down. The electron is deflected towards
(a) west (b) no deflection (c) east (d) north to south.
It will be convenient to use Fleming’s left hand rule here. You have to hold the fore-finger, middle finger and thumb of your left hand along mutually perpendicular directions so that the fore-finger points along the magnetic field and the middle finger along the direction of the conventional current (and hence opposite to the direction of the electron). The thumb will then give you the direction of deflection, which you can easily obtain as along the east [Option (c)]. You will find more multiple choice questions (with solution) at physicsplus: Magnetic Force on Moving Charges

Kerala Medical Entrance Test 2006- Two Questions on Heat

The following two questions appeared in the Kerala Medical Entrance 2006 test paper:
(1) A thermos flask made of stainless steel contains several tiny lead shots. If the flask is quickly shaken up and down several times, the temperature of lead shots
(a) increases by adiabatic process (b) increases by isothermal process (c) decreases by adiabatic process (d) remains the same (e) first decreases and then increases.
This is a simple question aimed at testing your understanding of a basic concept. In an adiabatic process, there is no heat transfer to or from the system. The system in the question is the lead shots contained in the thermos flask which is thermally insulated from outside. The temperature of the lead shots is therefore increased by adiabatic process [Option (a)].
(2) A body cools from 50˚C to 49.9˚C in 5 s. How long will it take to cool from 40˚C to 39.9˚C? Assume the temperature of the surroundings to be 30˚C and Newton’s law of cooling to be valid.
(a) 2.5 s (b) 5 s (c) 20 s (d) 10 s (e) 15 s
As per Newton’s law of cooling, the rate of cooling of a body is directly proportional to the mean excess of temperature of the body over the surroundings (if the absolute temperature of the body is nearly equal to the absolute temperature of the surroundings).
Therfore, we have (50 – 49.9)/5 α (49.95 – 30) and
(40 – 39.9)/t α (39.95 – 30)
Dividing the first one by the second, we obtain t/5 = 2, very nearly, so that the required time for cooling is 10 s.

Questions on Bohr Model of Hydrogen Atom

Questions based on the Bohr model of hydrogen atom are inevitable in any Medical and Engineering test paper. Consider the following two questions which appeared in A.I.I.M.S.- 2005 test paper:
(1) Solid targets of different elements are bombarded by highly energetic electron beams. The frequency (f) of the characteristic X-rays emitted from different targets varies with atomic number Z as
(a) f α √Z (b) f α Z² (c) f α Z (d) f α Z^3/2
As you might have noted, X-rays are produced by electron transitions from outer orbits to inner orbits. But atoms of high atomic number are required for the production of X-rays since the X-ray photon has much greater energy compared to light photon. The energy of the electron in an orbit is directly proportional to Z². [Note that in a hydrogen like atom, the energy is -13.6 Z²/n² electron volt]. The energy difference between levels also is directly proportional to Z². Since the energy difference is equal to hν where ‘ν’ is the frequency of the radiation emitted, the correct option is (b).
[More rigorous treatment shows that ν α (Z-b)² where b is a constant for a given spectral series].
(2) The ground state energy of hydrogen atom is -13.6 eV. What is the potential energy of the atom in this state?
(a) 0 eV (b) -27.2 eV (c) 1eV (d) 2 eV
The correct option is (b) since the potential energy is twice the kinetic energy. You should note that in all cases of central field motion under inverse square law attractive force, the total energy and potential energy are negative and the potential energy is twice the total energy.
Suppose we modify this question as follows:
The ground state energy of hydrogen atom is -13.6 eV. What is the kinetic energy of the electron in this state?
(a) -13.6 eV (b) -27.2 eV (c) 0 eV (d) 13.6 eV

The correct option is (d) since the kinetic energy is always positive and its magnitude is the same as that of the total energy. This is true in all cases of central field motion under an attractive inverse square law force, as in the case of the motion of a satellite around a planet.

You will find more multiple choice questions (with solution) at physicsplus: Questions on Bohr Atom Model

Optics - Questions on Reflection and Refraction

The average student is usually scared of questions in ray optics because of the wrong notion that the sign convention is some thing that adds to one’s confusion! The best thing to do is to work out as many questions as possible. You will definitely realize that there is nothing to worry about. Let us discuss the following questions:
(1) A glass slab of refractive index 1.5 and thickness 4.5cm is kept close to a concave mirror of focal length 20cm so that the face of the slab is perpendicular to the principal axis of the mirror. A point object is placed on the principal axis so that its image coincides with itself. Then, the distance of the object from the mirror is
(a) 40cm (b) 41.5cm (c) 43cm (d) 37cm (e) 47.5cm
If the glass slab is not interposed, the object is to be placed at the center of curvature of the mirror (at 40cm). When the glass slab is present, the distance of the object is to be increased by the apparent shift t - (t/μ) produced by the slab, so that the ray emerging from the slab appears to come from the center of curvature of the mirror.
Therefore, distance of the object = 40+ 4.5 – (4. 5/1. 5) = 41.5cm [option (b)].

(2) A glass sphere of radius 2cm and refractive index 1.5 has a small air bubble at a distance of 1.2cm from the surface through which it is viewed normally. Its apparent distance from the surface is
(a) 0.8cm (b) 1cm (c) 1.33cm (d) 1.6cm (e) 2.4cm
Don’t be tempted to pick out option (a), under the impression that this is similar to the normal refraction at a glass slab. You have to use the equation, μ₂/v - μ₁/u = (μ₂- μ₁)/R where μ₂= 1, μ₁= 1.5, R = -2cm and u = -1.2cm.
Note that we have imagined the ray from the object (air bubble) to be proceeding in the positive X-direction so that the object distance measured from the pole (which is imagined to be at the origin) to the object is negative. The radius of curvature of the spherical surface also is negative since we have to measure it from this pole to the centre of curvature. We leave the unknown quantity ‘v’ in the equation as it is, with out worrying about its sign.
Substituting these values, v = -1cm. The negative sign shows that the image, which is virtual, is on the same side of the refracting surface as the object is.
(3)An astronomical telescope has an eye piece of focal length 10cm. It gives a magnification of 20 in normal adjustment. The distance between the objective and the eye piece is
(a) 30cm (b) 60cm (c) 110cm (d) 200cm
In normal adjustment, magnification, m = fo/fe where fo and fe are the focal lengths of the objective and eye piece respectively. Therefore, fo = m.fe = 20´10 = 200cm.
Distance between objective and eye piece = fo + fe = 200+10 = 210cm.
(4) The plane faces of two identical plano-convex lenses each having a focal length of 50cm are placed against each other to form a usual biconvex lens. The distance from this lens combination at which an object must be placed to obtain a real, inverted image which has the same size as the object is
(a) 50cm (b) 25cm (c) 100cm (d) 40cm (e) 125cm
This simple question appeared in Kerala Engineering Entrance test paper of 2006. When two identical lenses are kept in contact, the focal length of the combination is reduced to half the value of each lens. (This is true even if the plane surface of one plano-convex lens is placed in contact with the curved surface of the other). The focal length of the combination therefore is 25cm.
A converging lens will produce a real, inverted image of the same size as the object when the object distance is 2f. So, the answer is 50cm.

You will find more multiple choice questions (with solution) from Optics here as well as at physicsplus: Questions (MCQ) on Refraction at Spherical Surfaces

Questions on Gravitation

You should definitely remember the following relations to ensure good score in gravitation:
(1) Acceleration due to gravity at a height ‘h’ is given by

g’ = GM/(R+h)², with usual notations.
Surface value of acceleration due to gravity, g = GM/R²
If ‘h’ is small compared to the radius ‘R’ of the earth, g' = g(1-2h/R)
(2) Acceleration due to gravity at a depth ‘d’ is given by g'' = g (1-d/R)
Note that this is true for all values of ‘d’.
(3) Gravitational potential energy of a mass ‘m’ at a height ‘h’ is given by U= -GMm/(R+h)
This can be written as U = -GMm/r where ‘r’ is the distance from the centre of the earth.

(4) Escape velocity from the surface of earth (or any planet or star),

v_e = √(2GM/R) = √(2gR)
Escape velocity from a height ‘h’ = √[2GM/(R+h)] = √[2g'(R+h]
(5) Kinetic energy and total energy of a satellite are equal in magnitude. But K.E. is positive where as total energy is negative. The potential energy of a satellite is negative and is equal to twice the total energy.( Note that this is true in all central field motion under inverse square law force, as for example, the energy of the electron in the hydrogen atom.)
In the case of a satellite of mass ‘m’ in an orbit of radius ‘r’:
Potential energy = -GMm/r
Kinetic energy = +GMm/2r
Total energy = -GMm/2r

(6) As per Kepler’s law, T² α r³
(7) Orbital speed ‘v’ of a satellite in an orbit of radius ‘r’ is independent of its mass and is given by v = √(GM/r) = √(g'r) where g' is the acceleration due to gravity at the orbit and M is the mass of the earth (or planet).
Let us now discuss the following question which appeared in the Kerala Medical Entrance Test paper of 2002:
The escape velocity of a body on an imaginary planet which has thrice the radius of the earth and twice the mass of the earth is (where v_e is the escape velocity on the earth)
(a) √(2/3).v_e (b) √(3/2).v_e (c) √(2).v_e/3 (d) 2v_e/√3 (e) 2v_e/3
We have v_e = √(2GM/R). Replacing R with 3R and M with 2M, we obtain the answer as√(2/3).ve [option (a)].
Consider now the following question which may confuse some of you:
The orbital velocity of an artificial satellite near the surface of the moon is increased by 41.4%. The satellite will
(a) move in an orbit of radius greater by 41.4% (b) move in an orbit of radius twice the original value (c) move in an elliptical orbit (d) fall down (e) escape into outer space
The correct option is (e). The orbital speed of any satellite moving round any heavenly body is √(GM/r) where as the escape velocity is √(2GM/r). This means that the escape velocity is √2 times the orbital speed or 1.414 times the orbital speed. Therefore, when the orbital speed is increased by 41.4% the satellite will escape into outer space.
Consider now the question which appeared in the Kerala Engineering Entrance Test paper of 2001:
The orbital speed of an artificial satellite very close to the surface of the earth is V0. Then the orbital speed of another artificial satellite at a height equal to 3 times the radius of the earth is
(a) 4V0 (b) 2V0 (c) V0 (d) 0.5V0 (e) 2V0/3
We have V0 =√(GM/R). At a height equal to three times the radius of the earth, the orbital velocity is obtained by replacing R with R+3R = 4R. The answer is 0.5R [option (d)].
The following simple question appeared in the IIT 2001 test paper:
A simple pendulum has a time period T1 when on earth’s surface, and T2 when taken to a height R above the earth's surface, where R is the radius of the earth. The value of T2/T1 is
(a) 1 (b) √2 (c) 4 (d) 2
The required ratio is [2π√(L/g’)] / [2π√(L/g)] = √(g/g’). But g = GM/R^2 and g’ = GM/(2R)^2 so that g/g' = 4. The answer therefore is 2 [option(d)].

Consider now the following question which appeared in H.P.P.M.T.2005:
If a body of mass ‘m’ is raised from the surface of the earth to a height ‘h’ which is comparable to the radius of the earth R, the work done is
(a) mgh (b) mgh[1-(h/R)] (c) mgh[1+(h/R)] (d) mgh/[1+(h/R)]
Note that ‘g’ is the acceleration due to gravity on the surface of the earth. The work done for raising the body is the difference between the gravitational potential energies at the height ‘h’ and at the surface. Therefore, work done, W = -GMm/(R+h) – (-GMm/R) where M is the mass of the earth. Therefore, W = GMm/R - GMm/(R+h) = mgR – mgR/[1+(h/R)], on substituting g=GM/R².
Thus, W = mgR[1- 1/1+(h/R)] = mgh/[1+(h/R)]

Questions from Optics- Cartesian Sign Convention

The sign convention adopted widely in Optics is the Cartesian convention. The ray incident on the curved surface is to be considered as proceeding in the positive X-direction and you have to measure all distances from the pole, which is supposed to be the origin.
Occasionally, you may be given a ray diagram in which the incident ray may be proceeding from right to left. To avoid confusion, imagine that the direction of the incident ray is still in the positive X-direction. You can even redraw the diagram to make the incident ray proceed from left to right if you want. The signs given to the distances are as in the Cartesian coordinate system: pole to right positive and pole to left negative. Distances measured (from pole) upwards are positive and those measured downwards are negative but you will mostly encounter problems with leftward and rightward measurements.
While solving problems, you should apply the signs to all known quantities. The unknown quantities are left as they are in the formulae. You will be able to arrive at conclusions by interpreting the sign of the unknown quantity you finally arrive at as the answer. For instance, if the distance of an image is obtained as negative, you will immediately understand that the image is on the same side of the curved surface as the object is.
Let us consider the following M.C.Q.:
A convex lens made of crown glass of refractive index 1.5 has focal length 20 cm. What will be its focal length within water (refractive index 4/3)?
(a) 10 cm (b) 20 cm (c) 40 cm (d) 60 cm (e) 80 cm
Writing lens maker’s equation 1/f = [(μ₂/μ₁) -1] [(1/R₁) - (1/R₂)] for the two cases, we have,
1/20 = [1.5-1] [(1/R₁) - (1/R₂)] for the first case, where f = +20cm (for convex lens), μ₂ = 1.5 and μ₁ = 1 (for air) and
1/f = [1.125 – 1] [(1/R₁)-(1/R₂)] for the second case where μ₂= 1.5 and μ₁ = 4/3 (for water).
Note that we have ignored the signs of the unknown quantities f, R₁ and R₂. On dividing the first equation by the second, we obtain f = 80 cm[option (e)].
The result shows that within water, the lens is still a converging lens. If the liquid has refractive index more than that of the lens, the lens will become diverging within the liquid. Let us consider such a case:
A converging lens of focal length 20cm is made of glass of refractive index 1.5. How will this lens behave if it is immersed in a liquid of refractive index 1.6?
(a) As a converging lens of focal length 80cm (b) As a diverging lens of focal length 80cm (c) As a diverging lens of focal length 120cm (d) As a diverging lens of focal length 160cm (e) As a converging lens of focal length 120cm
The correct option to this question is (d). You can check this by writing the lens maker’s equation for the two cases as in the previous question. The first equation is unchanged: 1/20 = [1.5-1] [(1/R) - (1/R₂)]. The second equation is
1/f = [0.9375 – 1] [(1/R₁) - (1/R₂)] since μ₂/μ₁) = 1.5/1.6 = 0.9375.
Dividing the first equation by the second, we obtain f = -160cm. As we get a negative value for the focal length, the lens behaves as a diverging lens within the given liquid [option (d)].
Let us discuss one more question:
The plane face of a planoconvex lens is silvered. If the refractive index of the material of the lens is μ, and the radius of curvature of its curved face is R, then the system behaves like a concave mirror of radius of curvature
(a) Rμ (b) R/μ (c) R/ (μ-1) (d) R/2(μ-1) (e) R(μ-1)
When one surface of a lens is silvered, the rays of light entering through the un-silvered surface are refracted first, reflected by the silvered surface next and finally are once more refracted. The effective focal length (F) of the system is given by
1/F = 1/f + 1/fm + 1/f where ‘f’ is the focal length of the un-silvered lens and fm is the focal length of the silvered surface which makes a mirror. In the present problem since the silvered surface is plane, fm is infinity so that the above equation becomes
1/F = 1/f + 0 + 1/f = 2/f. Therefore, F = f/2.
But we have for the original un-silvered lens, 1/f = (μ – 1) [(1/R₁) - (1/R₂)] where R₁ = R and R₂ = infinity. Therefore, f = R/(μ – 1)
Since F = f/2, the system has a focal length of R/2(μ – 1).The radius of curvature of a concave mirror is twice its focal length. Therefore, the system behaves like a concave mirror of radius of curvature R/(μ – 1). [Option (c)]. You will find multiple choice questions (with solution) on refraction at plane surfaces here as well as here

Questions on Rotational motion

In most of the Medical and Engineering Entrance test papers you will encounter at least a couple of questions on rotational motion. Let us consider the following questions:

(1) A solid cylinder initially at rest rolls down an inclined plane of angle θ and height ‘h’ without slipping. The linear velocity with which it will reach the bottom of the plane is

(a) √(3gh/4) (b) √(4gh/3) (c) √(4ghsinθ/3) (d) √(5gh/4) (e) √(2ghsinθ/3)

If ‘v’ and ‘ω’ are the linear and angular velocities respectively, ½Mv² + ½Iω² = Mgh where I is the moment of inertia and M is the mass of the cylinder. Substituting I = ½ MR² and ω = v/R , we get v = √(4gh/3). Note that the angle θ mentioned in the problem is just a distraction.

(2) A simple pendulum bob of mass ‘m’ is drawn to one side so that the string is horizontal. It is then let free. When it crosses the mean position, the tension in the string is

(a) mg (b) 0.5mg (c) 1.5mg (d ) 3mg (e) 5mg

In problems of this type, you should note that the centripetal force (which is equal to mv²/r) acting on the body executing circular motion is the net force on the body. Therefore, centripetal force, mv²/r = T – mg, where r is the length of the pendulum and T is the tension in the string.Therefore, T= mv²/r + mg. But, ½ mv² = mgr, on equating the initial gravitational potential energy of the bob to its kinetic energy in the mean position. From this, mv²/r = 2mg and hence T = 2mg + mg = 3mg.

Let us consider the following two questions involving the rotation of the earth:
(1) If the radius of the earth is changed to 1/√3 times the present value, the duration of the day (in hours) will be
(a) 72 (b) 41.6 (c) 24 (d) 12 (e) 8
This question is set to check your understanding of the law of conservation of angular momentum: I₁ω₁= I₂ω₂ where I₁and I₂ are the moments of inertia and ω₁ and ω₂ are the angular velocities of the earth before and after the contraction respectively. Substituting for I₁ (= 2MR²/5) and I₂ [= 2M (R²/3)/5] we obtain ω₂ = 3ω₁. Since the angular velocity changes to 3 times the initial value, the spin period of the earth (T= 2π/ω) changes two one-third of the initial value. So, the duration of the day will become 24/3 = 8 hours.
Questions of this type are often found in Medical and Engineering Entrance Test papers. Generally, if the radius of the earth becomes ‘n’ times the present value, the duration of the day becomes 24n² hours. Remember this equation and write the answer in no time!
(2) If your weight while standing on the earth’s surface at the equator is to become zero, the earth should spin at nearly ------ times the present speed.
(a) 12 (b) 14 (c) 17 (d) 24 (e) 37
This is a simple question. If you are to become weightless due to the spin of the earth, the gravitational pull on you is to be balanced by the centrifugal force so that, mg = mRω². From this ω=√(g/R) and the spin period T=2π/ω=2π√(R/g). On substituting for R = 6400 km and g = 9.8ms^-2, the period works out to be 84.6 minutes. This is one-seventeenth the present period of 24 hours. So, the earth should spin at 17 times the present speed. [Option (c)].

Two Questions from Electrodynamics

(1) A straight conductor carries a current of 10A. An electron traveling with a speed of 2.5×10^6m/s parallel to the conductor at a distance of 1cm from the conductor experiences a force of
(a) 8×10^-17N (b) 8×10^-18N (c) 8×10^-19N (d) 4×10^-20N (e) 4×10^-18N
Force on the electron, F=qvB, where B= μoI/2πr with usual notations.
Note that the direction of the magnetic field produced by the conductor is perpendicular to the direction of motion of the electron since the magnetic field lines are in the form of concentric circles.
Therefore, F= (1.6×10^-19×2.5×10^6×4π×10^-7×10) / 2π×0.01 = 8×10^-17N.
(2) A galvanometer having resistance 3Ω is converted into an ammeter by connecting a 3Ω shunt resistance across it. In order to double the range of this ammeter, the additional shunt resistance to be connected across it is
(a) 3Ω (b) 2.5Ω (c) 2Ω (d) 1.5Ω (e) 6Ω
With usual notations, Ig G = (I-Ig)S. Since G = S =3Ω, Ig = I/2. If S′ is the additional shunt required, the effective shunt for doubling the range is SS′/(S+S′) . Therefore, when the range is doubled, IgG = (2I-Ig) SS′/(S+S′) . Substituting G=S=3 and Ig= I/2 , 3S'/(3+S') =1. Therefore,S'=1.5Ω.
Instead of following the above mathematical steps, you can easily arrive at the answer as follows:
The ammeter with the original shunt has an effective resistance of 1.5Ω. If you want to pass twice the maximum allowed current into the ammeter, half of this doubled current has to be diverted through another path. So you have to provide a shunt path of resistance 1.5Ω.

An Interesting Post on Friction

Here is a useful link which will take you to an interesting post on friction:
physicsplus: Friction Moves the Car and Friction Stops the Car

Questions on Simple Pendulum

The period of oscillation of a simple pendulum is given by the simple equation,
T = 2π√(L/g).
Questions based on this equation can be seen in test papers. The following question appeared in the I.I.T. screening test of 2005:

The point of suspension of a simple pendulum with normal time period T₁ is moving upward according to the equation, y=kt² where k=1 m/s². If the new time period is T, the ratio T₁²/ T² will be

(a) 2/3        (b) 5/6        (c) 6/5        (d) 3/2

             This is a simple question. But you should note that the acceleration due to gravity ‘g’ is to be replaced by the net acceleration (g+a) since the pendulum as a whole is moving up with an acceleration ‘a’ which is obtained by differentiating the equation y = kt² twice. Therefore, a = 2k = 2 since k=1. The new period is given by,

            T = 2π√[L/(g+a)] = 2π√[L/(10+2)] = 2π√(L/12).

The normal period of the pendulum is

            T1 = 2π√(L/10).

Therefore, T₁²/ T² =12/10 = 6/5  [Option (c)]

Let us consider another question in which en electric force modifies the effective weight of the bob of the pendulum, thereby changing the period of oscillation:
A simple pendulum of length ‘L’ has a small spherical bob of mass ‘m’ that carries a positive charge ‘q’. The pendulum is located in a uniform electric field ‘E’ directed vertically upwards. If the electric force is less than the gravitational force, the period of oscillation of this pendulum is
(a) 2π√(L/g) (b) 2π√[L/(g-E)] (c) 2π√[L/(g+Eq/m)] (d) 2π√[L/(g-Eq/m)]
(e) 2π√[L/(g+E)]
Here also you have to replace ‘g’ (in the expression for the period) by the net acceleration, as in the previous question. But the net acceleration in the present case is (g-a) where a = Eq/m, which is the acceleration produced by the electric force Eq. Therefore ‘g’ is to be replaced by (g-Eq/m). The correct option therefore is (d).
Note that the real weight of the bob is mg. The apparent weight of the bob is (mg-Eq) since the electric force is upwards. The net downward acceleration therefore is (g-Eq/m).
A simple pendulum will not work on an artificial satellite orbiting round the earth since the pendulum bob becomes weightless and hence there is no restoring force mgsinθ. But you can use a spring loaded with a mass as an oscillator even on an artificial satellite or for that matter, even in a region of space where there is no gravitational force. The period of oscillation of such a spring-mass system, as you might be remembering is
T = 2π√(m/k), where m is the mass and k is the spring constant.
This equation is devoid of g and so the system works even in weightless situations.
Now suppose that the bob of a simple pendulum of length ‘L’is immersed in a non-viscous liquid of density equal to one-tenth the density of the material of the bob. The apparent weight of the bob is now reduced to nine-tenth of the real weight(because of the upthrust of the liquid). The period of oscillation of the pendulum therefore increases as
T = 2π√(10L/9g)
[The above equation is easily obtained if you remember that the mass of the bob is vρ and the apparent weight of the bob is v(ρ-σ)g so that the net value of the downward acceleration of the bob is v(ρ-σ)g /vρ = (1- σ/ρ)g = (1- 1/10)g = (9/10)g.]
In the case of a spring-mass system, there is no change in the period if the oscillating mass is immersed in a non-viscous liquid, since the period is independent of ‘g’.

Simple Pendulum of Infinite Length
The period of oscillation of a simple pendulum, as you know, is given by

T=2π√(l/g), with usual notations. If the length of the pendulum is not negligible compared to the radius(R) of the earth, the period is given by
T = 2π√[Rl/(R+l)g]. This equation shows that in the case of a simple pendulum of infinite length(or, to be more realistic, in the case where the length is large compared to the radius of the earth), the period is
T = 2π√(R/g)
On substituting for R = 6400 km (=64×10^5m) and g = 9.8m/s^2, the period works out to be 5078seconds or, 84.6 minutes.
Remember the above equation. The period of oscillation of a stone dropped into an imaginary hole drilled along the diameter of the earth and the orbital period of a satellite moving close to the earth’s surface also are given by this equation.

Elastic Potential Energy

When you elongate or contract a rod or wire by exerting a force, you do work. This work is stored as elastic potential energy in the rod or wire. The elastic potential energy per unit volume is easy to remember and is equal to ½ stress×strain. Since the Young’s modulus Y = stress/strain, we can modify the above expression as ½ Y×strain². Another form of the same expression is ½ (stress)²/Y.

Consider the following M.C.Q. which appeared in the Kerala Engineering Entrance test paper of 2006:

A work of 2×10^-2 J is done on a wire of length 50cm and area of cross section 0.5mm². If the Young’s modulus of the material of the wire is 2×10¹⁰ N/m², then the wire must be

(a) elongated to 50.1414cm (b) contracted by 2mm (c) stretched by 0.707mm (d) of length changed to 49.293cm (e) of length changed to 50.2cm

Since the total work done is involved in this prblem, we write,

½ (Y×strain²) ×volume = 2×10^-2

Here, strain = δ/0.5 where ‘δ’ is the elongation (or contraction) and volume = AL = (0.5×10^-6) ×0.5

Substituting proper values, δ works out to 1.414×10^-3 m = 1.414mm = 0.1414cm. The wire therefore elongates to 50.1414cm [option(a)].

An expression you should remember for obtaining the total work done in stretching or contracting a rod or wire through ‘l’ by exerting a force ‘F’ is, W = ½ F × l.

Breaking Strength and Breaking Stress

The breaking strength of a given wire depends on its area of cross section where as the breaking stress is a constant for a given material. Consider the following M.C.Q.:
A cable of length 10m and diameter 2cm can support a maximum load of 800 kg. If the length and the diameter of the cable are reduced to 5m and 1cm respectively, it will be able to support a maximum load of
(a) 200kg (b) 400kg (c) 800kg (d) 1600kg (e)100kg
The breaking strength is independent of the length but is directly proportional to the area of cross section. This follows from the expression for Young’s modulus (Y):
Y = Stress/strain. It is the strain which determines the breaking point of a cable.The strain at the breaking point is a constant for a given material. Since the Young’s modulus is a constant for a given material, the breaking stress also is a constant for a given material. Since the breaking stress is the ratio of the breaking strength to the area of cross section, it follows that the breaking strength is directly proportional to the area of cress section.
In the above problem, the breaking strength of the cable of diameter 2cm is 800 kgwt or(800×g) newton. Since the breaking stress is constant for the material of the cable, we can write, (800×g)/ (π×0.02^2) = mg/(π×0.01^2) where ‘m’ is the load the cable of half the diameter can support. Therefore, m = 200kg [option (a)]. It will be more convenient to write, 800/2^2 = m/1^2 to find ‘m’.
Suppose the breaking stress of a steel cable is ‘s’. What is the breaking stress of a steel cable of double the length and three times the diameter?
The answer, as you know, is ‘s’ since the breaking stress is a constant for a given substance.
Here is a very simple question which may mislead you if you are overconfident:
The Young’s modulus of a piano wire is Y. The Young’s modulus of another piano wire of half the thickness and twice the length is
(a) 2Y (b) 4Y (c) 8Y (d) Y/8 (e) Y
The correct option is (e) since the Young's modulus of a given substance is a constant.

You may visit physicsplus.blogspot.com for more multiple choice questions with solution.

Two Questions from Modern Physics

(1) The energy of a photon is 20eV. Its momentum in kg m/s is
(a) 2.56×10^-27 (b) 5.33×10^-27 (c) 1.066×10^-26 (d) 2.13×10^-26 (e) 3.18×10^-26
Since E=mc^2, momentum of the photon, p = E/c = (20×1.6×10^-19)/(3×10^8). Note that we have converted the energy in eV into joule. The answer is 1.066×10^-26 kg m/s given in option (c).
(2) The wave length associated with an electron having kinetic energy 6eV is
(a) 9A.U. (b) 5A.U. (c) 2.5A.U. (d) 1.5A.U. (e) 0.5A.U.
In the case of electrons, de Broglie wave length, λ = √ [ 150/V] A.U. where V is the accelerating voltage for the electron (= 6 volt since the energy is 6 eV).
Therefore, λ = √25 = 5 A.U.

Two Questions from Properties of Matter:
The following question appeared in the Kerala Engineering Entrance test paper of 2006:
The pressure inside two soap bubbles is 1.01 and 1.02 atmosphere respectively. The ratio of their respective volumes is
(a) 2 (b) 4 (c) 6 (d) 8 (e) 10
To the surprise of this author, a comparatively bright student omitted this question, which is quite simple. You know that the excess of pressure inside a bubble is 2T/r, where T is the surface tension and r is the radius. The ratio of the excess pressures inside the bubbles is P1/P2 = r2/r1. But, P1/P2 =0.01/0.02. [Since the actual pressures are 1.01 and 1.02 atmosphere]
So, we have r2/r1 = 1/2. The ratio of volumes, V1/V2 = (r1/r2)^3 = 2^3 = 8.
Consider now the following question which appeared in Kerala Medical Entrance test paper of 2006:
To what depth below the surface of sea should a rubber ball be taken so as to decrease its volume by 0.1%? [Take: Density of sea water = 1000kg/m^3, bulk modulus of rubber = 9×10^8 N/m^2, acceleration due to gravity = 10m/s^2]
(a) 9m (b) 18m (c) 180m (d) 90m (e) 900m
We have bulk modulus B = P/(dv/v) so that P = B(dv/v) = (9×10^8) ×0.001 = 9×10^5 pascal.
Therefore, hdg = 9×10^5 from which, h = (9×10^5)/(1000×10) = 90m. [Option (d)]

Two Questions involving Energy and Power

(1) A bullet of mass 100g penetrates a distance of 10cm through a fixed block of mass 2kg. If the block is free to move, the distance penetrated will be nearly
(a) 3.5cm (b) 4.5cm (c) 5.5cm (d) 7.5cm (e) 9.5cm
If ‘F’ is the retarding force offered by the block and ‘s’ is the distance of penetration when the block is fixed, we have
Fs = ½ mu^2 ……………..(1)
where ‘m’ is the mass and ‘u’ is the initial velocity of the bullet. If ‘x’ is the distance of penetration when the block is free to move, we have
Fx = ½ mu^2 - ½ (M+m) v^2 where ‘M’ is the mass of the block and ‘v’ is the common velocity of the bullet and the block after the impact. Evidently, v = mu/(M+m) from the momentum conservation law so that we have
Fx = ½ mu^2 - ½ (M+m) [mu/(M+m)]^2
Simplifying, Fx = ½ Mmu^2 /(M+m) ………….(2)
Dividing eq(2) by eq(1) we get x/s = M/(M+m) so that x = Ms/(M+m) = 2×0.1/(2+0.1) = 0.095m = 9.5cm.
(2) An engine delivering constant power displaces a large block through 40cm in 4 seconds. What will be the displacement of the block in 16seconds?
(a) 1.6m (b) 3.2m (c) 4.8m (d) 6.4m (e) 8m
If the power is constant, the displacement will be proportional to t^(3/2) as shown below:
Power P = Fv = m(dv/dt)×v with usual notations. Since the power is constant (k) we have m(dv/dt)×v = k so that v(dv) = k(dt)/m. Integrating, we get
½ v^2 = kt/m. Therefore, v α√t. Since s=vt the displacement ‘s’ is proportional to t√t. Remember this: If power is constant, displacement is directly proportional to t^(3/2)
In the above problem therefore we can write
0.4/x = (4√4)/(16√16) =8/64, from which x = 3.2m

Multiple Choice Questions on Friction:

The following question appeared in the Physics paper of A.I.E.E.E.-2005:

The upper half of an inclined plane with inclination Ф is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for lower half is
(a) tanФ (b) 2tanФ (c) 2cosФ (d) 2sinФ

You have to use the equation of linear motion, v² = u² + 2as for both parts of the motion. For the smooth half of the incline, we have v² = 0 + 2gsinФ×s and for the rough half we have 0 = v² +2(gsinФ - μgcosФ)×s. Combining these two equations, we get
0 = 2gsinФ×s + 2(gsinФ - μgcosФ)×s, from which 2sinФ = μcosФ
Therefore, μ = 2tanФ [Option (b)]
Consider the following MCQ:

A car of mass 1000kg moves on a circular track of radius 20m. If the coefficient of friction is 0.64, then the maximum velocity with which the car can move is
(a) 15m/s (b) 11.2m/s (c) 20m/s (d) 18m/s (e) 22.4m/s
This simple question appeared in the Kerala Engineering Entrance Test paper of 2006. As the frictional force supplies the centripetal force required for the circular motion, we have μmg = mv² /r so that v = √(μrg) = √(0.64×20×9.8) = 11.2m/s

Let us discuss two more questions involving friction:
A coin of mass ‘m’ is placed on a rough horizontal turn table with coefficient of limiting friction ‘μ’. The distance of the coin from the axis of the turn table is ‘r’ and the turn table is turning with angular velocity ‘ω’. The maximum value of ω so as to keep the coin intact on the turn table is
(a) √(μg/r) (b) √(μgr) (c) μgr (d) √(μr/g) (e) μgr²
It is the frictional force that prevents the coin from sliding outwards under the action of the centrifugal force. Therefore we equate the limiting value of the frictional force to the centrifugal force (magnitudes): μmg = mrω² from which ω = √(μg/r). The correct option is therefore (a).
Suppose you are not asked to find the maximum value of ω in the above problem. Instead, you are asked to find the frictional force at the angular velocity ω, as in the modified question below:
A coin of mass ‘m’ is placed on a rough horizontal turn table with coefficient of limiting friction ‘μ’. The distance of the coin from the axis of the turn table is ‘r’ and the turn table is turning with angular velocity ‘ω’. If the coin remains intact on the turn table, the frictional force between the coin and the surface of the turn table is
(a) μmg (b) zero (c) mg (d) mrω² (e) mrω
Nothing is mentioned about the limiting equilibrium of the coin and therefore, the self adjusting frictional force just balances the centrifugal force mrω²
. The correct option therefore is (d).

Two questions from Communication Systems

Questions on topics in Communication Systems are generally simple and not at all time consuming. You should never omit them. Consider the following:
(1) Photo diodes used as light detectors in optical communication systems are operated in the reverse biased manner because
(a) forward biasing will damage the photo diode (b) power requirement is small in reverse biased mode (c) it is more convenient to measure reverse current (d) reverse current alone is affected by illumination (e) the fractional change in reverse current is much greater than the fractional change in forward current.
You know that the forward current is typically of the order of milliamperes while the reverse current is of the order of micro amperes. When light is incident on the photodiode, electrons and holes are produced in equal number, contributing equally to forward current and reverse current. Since the existing reverse current is a small current compared to the forward current, the change in reverse current will be significant compared to the reverse current itself. The change in reverse current is therefore much easier to detect compared to the change in forward current. The correct option therefore is (e).
(2) A TV transmitter tower has a height of 80m. If the range is to be doubled, the height of the tower is to be increased by
(a) 160m (b) 80m (c) 240m (d) 320m (e) 33m
With usual notations, range = √(2Rh). Therefore, to double the range, the height ‘h’ is to be made 4 times (320m). The increment in height is 240m [Option (c)]. In your hurry to answer this simple question, don’t fail to note that it is the increase in height that is asked for.